반응형
itutorial - A rectifier diode (rectifier) is a PN junction diode which is used to rectify ac electric current ( alternating current ) into dc electric current ( direct current ).
Rectifiers have two types of rectification, namely:
- Half wave rectifier : This is a rectifier using one diode which only rectifies the positive half wave, the negative half wave is blocked or discarded.
- Full wave rectifier : This is a rectifier that uses two or four diodes to rectify the full wave so that the negative half-wave ac current is reversed into a positive half-wave which produces a full-wave dc current.
A. Half Wave Rectifier
A half wave rectifier with one diode is shown in Figure 1. In the example an ideal diode is used to facilitate understanding in calculating the output voltage of the half wave rectifier.
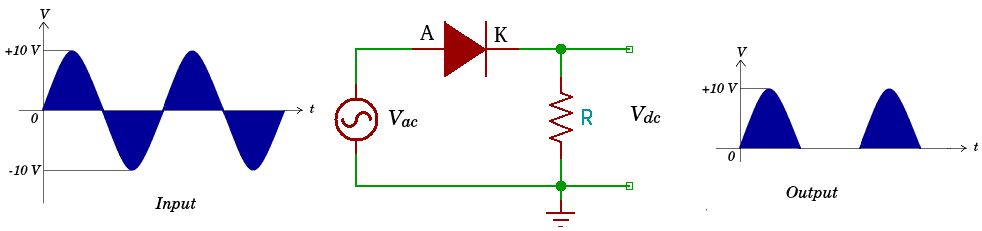 |
| Figure 1. Half wave rectifier |
Figure 1 shows that the ac input voltage has a peak voltage Vp of 10 Volts . When an ac voltage is passed through the half wave rectifier circuit, the negative half wave -10 Volts will be cut off so that at the output there is only the positive half wave.
To calculate the dc output voltage we need to understand some basic theory of sinusoidal signal form as shown in Figure 2 as follows:
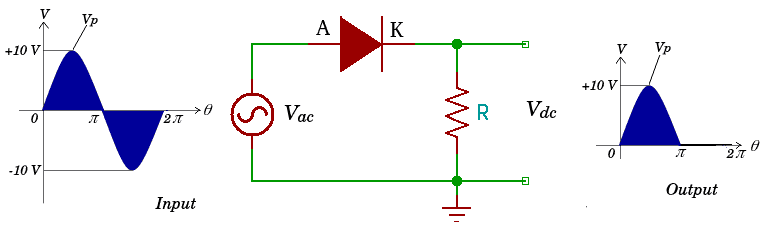 |
| Figure 2. Half wave ac to dc voltage conversion |
Finding the value of the dc output voltage is to use an integral where in general the integral is to find the area of the blue area (positive half wave) which is averaged in one wave cycle, namely 2 π so that the dc output voltage can be written as follows:

If you are still confused about why the formula is as written above, here is an explanation which might provide an understanding of the formula above:
- The formula above uses an angle approach where θ = ω.ts so there is no need to analyze the value of ω .
- The integral ∫ V p sin θ dθ aims to calculate the area of the sine function in the blue area. V p is the peak or highest voltage in the sine function.
- The integral limit of π and 0 is to calculate the area of the positive half-wave blue sine function region from 0 to π. The voltage V p 0 at the limit of π to 2 π because the current is not passed by the diode. This limit of π is in angles. The value of π = 180 degrees.
- The divisor 2 π ( 1/2 π ) is the average area in one period where one period is 2 π . In this average π is in radians where 180 degrees is equal to π .
- DC voltage ( V dc ) is a positive half-wave voltage averaged over one period.
The solution to the V dc formula is as follows:





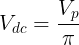

Because the definition of dc voltage in a half-wave rectifier is the average output voltage , the dc voltage is often referred to as average voltage ( V avg ) so that the output dc voltage of a half-wave rectifier is often written as average voltage.

The amount of dc current flowing through the resistor is:




Because the dc current value is the average value of the current in one period, the dc current is also called the average current:

Figure 3 shows that the output frequency of the half wave rectifier is the same as the input frequency . In one period the ac input signal has one peak voltage + Vp and one peak voltage -Vp , so that in one period it only has one positive peak voltage or only one negative peak voltage. The output voltage of the half-wave rectifier circuit has one peak voltage Vp in one period so it can be concluded that the output frequency of the half-wave rectifier is the same as the input frequency of the ac signal.

RMS ( Root Mean Square ) Value
The half wave rectifier output still has ripples (not constant dc) so it has an RMS value where the RMS value is always greater than or equal to the dc value ( V RMS ≥ V dc ). The RMS value can be used to find the ripple factor value .
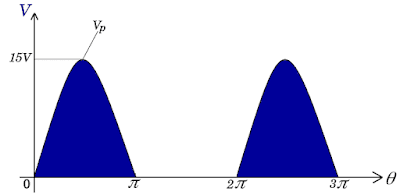 |
| Figure 3. Half wave rectifier output |
RMS voltage ( V rms ) half wave rectifier
Based on the definition of RMS, namely Root Mean Square , the RMS value of the half-wave rectifier output can be written as the root of the average voltage squared .




From the trigonometry formula it is found that:



So V RMS can be continued as:





In reality, the diode has a barrier voltage of 0.7 Volts so the V RMS formula can be written as follows:

RMS current ( I RMS ) half wave rectifier
To find the value of the RMS current ( I RMS ) is to divide the voltage V RMS by the resistance in the rectifier circuit:





The amount of I RMS on a diode with a barrier voltage of 0.7 Volt is:

if the maximum current I max is:

so,


DC efficiency of half wave rectifier
From the RMS value and dc value, the efficiency of the half wave rectifier can be calculated where the efficiency is the ratio between the dc power value and the RMS power value. If the diode is assumed to be an ideal diode to simplify calculations, then the efficiency of the half wave rectifier can be written:





The efficiency of the half-wave rectifier is 40.4%.
Ripple Factor half wave rectifier
Ripple or ripple is an ac component that occurs in the component or dc value of the rectifier output . The ac component is undesirable in a rectifier circuit so the benchmark for the effectiveness of a half wave rectifier circuit is the ripple factor (r) which is defined as the ratio of the RMS ripple value and the dc value . The smaller the ripple factor value, the smaller the component or ripple .
When looking for the ripple factor, you have to look for the value of the RMS ripple current ( I rRMS ) because the RMS current ( I RMS ) can be defined as the sum of the dc current and the RMS ripple current as follows:








From the definition of ripple factor , the ripple factor (r) can be written as follows:



All the explanations about half wave rectifiers above show that the output has several voltages, namely peak voltage ( V P ), middle RMS ( V RMS ) and dc voltage ( V dc ).
 |
| Figure 4. Output voltage Vp , V RMS and V DC . |
B. Full Wave Rectifier
A full wave rectifier can be built using four PN junction ( bridge ) diodes or using just two diodes. This depends on the application, such as if a full wave rectifier is used to transmit the ac signal output from the center trap transformer (CT), then only two diodes are used.
If a full wave rectifier is used to rectify the transformer output AC signal without CT then it uses four diodes or a diode bridge as shown in Figure 5.
 |
| Figure 5. Full wave rectifier using bridge diode |
The transformer output voltage at terminal ab has a peak voltage Vp of +15 Volts and -15 Volts. When the half-wave voltage V ac is positive, electric current flows from terminal a to terminal b through diode D 2 , resistor R and diode D 3 . By flowing electric current through the resistor, there is a positive half-wave voltage on the resistor with a peak voltage Vp of 15 Volts.
When the voltage V ac of the transformer is in the negative half wave position, electric current flows from terminal b to terminal a through diode D 4 , resistor R and diode D 1 so that the negative half wave ac becomes a positive half wave. When there is an electric current flowing through the resistor, there is a positive half-wave voltage on the resistor with a peak Vp of 15 Volts.
With the explanation above, the output voltage signal form of a full wave rectifier is shown as in Figure 5 or Figure 6 below.
 |
| Figure 6. Full wave rectifier signal form |
Calculating the dc output voltage of a full wave rectifier is similar to calculating the dc voltage of a half wave rectifier. It's just that in a full wave rectifier in one period there are two sine function integrals which are added together, namely the average of the sine integrals with the limit 0 to π is added to the average of the sine function integrals with the limit π to 2 π . This is because the one-period signal in Figure 6 cannot be directly integrated using the sine function because the waveform is no longer a full sine in one period. So, to find the dc voltage, you can use the formula for two integral half-period positive sine waves which are added as follows:






Because the dc voltage value is an average value, the dc voltage V dc is also often referred to as the average voltage V avg :

Figure 6 also shows that the output frequency of a full wave rectifier in one period ( 2π) is twice the input frequency . This is because in one period the signal has two peak voltages Vp .
The amount of dc current flowing in the full wave rectifier circuit ( I dc ) is the dc voltage divided by the resistance of the full wave rectifier.



Because the dc current of a full wave rectifier is the average value of the current flowing, it can be written as follows:

RMS value of full wave rectifier
The output of a full wave rectifier still has ripples so it has an RMS value like a half wave rectifier, but the RMS value of a full wave rectifier has a greater value because in one period it has twice the frequency than a half wave rectifier.
 |
| Figure 7. V RMS full wave rectifier |
RMS voltage ( V RMS ) full wave rectifier
The RMS output voltage value of a half-wave rectifier can be written as the root of the average voltage of the full-wave rectifier squared.

from the trigonometry formula where:

so it can be written as:






so the magnitude of the voltage V RMS of the full wave rectifier is:

RMS current ( I RMS ) full wave rectifier
The magnitude of the RMS current of a full wave rectifier depends on the resistance in the rectifier circuit so that the magnitude of I RMS is the RMS voltage divided by the resistance.




Full wave rectifier efficiency
The efficiency of a full wave rectifier is the ratio of the dc power value to the RMS power value. To simplify calculations, the diode is assumed to be an ideal diode so that the efficiency of a full wave rectifier can be written as follows:



So the efficiency of a full wave rectifier is 0.812 or 81.2% .
Ripple Factor full wave rectifier
From the explanation of the half wave ripple factor above, you can immediately find the full wave ripple factor (r) as follows:


Where :
I RMS : RMS current.
I rRMS : RMS ripple current is the ripple component in a full wave rectifier.
I dc : dc current in a full half wave rectifier.



So the magnitude of the ripple factor (r) of a full wave rectifier is:



To eliminate ripple reduction , it is necessary to add an RC filter which is discussed on the Rectifier Diode page using an RC filter .
Conclusion :
From the calculations above, the rectifier diode formula without using a capacitor can be seen in the following table:

V P is the peak voltage or maximum voltage.
I P is the peak current or maximum current.
반응형
'Eelektronika' 카테고리의 다른 글
| JFET (Junction Field Effect Transistor) (0) | 2024.04.26 |
|---|---|
| Op-amps (0) | 2024.04.26 |
| JFET (Junction Field Effect Transistor) (0) | 2024.04.26 |
| N-MOSFET Amplifier Common Source (0) | 2024.04.26 |
| PWM Arduino Uno (0) | 2024.04.26 |